


OPTIMIERUNG
In unserem Leben versuchen wir ständig bewusst und unbewusst alles optimal zu gestalten. Sei es die eigenen Ausgaben zu minieren, den eigenen Wohlstand zu maximieren, seine zeitlichen Präferenzen optimal zu setzen oder selbst beim Brettspielabend den besten Zug zu finden. Selbst bei diesen einfachen Beispielen offenbart sich uns die Komplexität eines Optimierungsproblems, denn die Ausgaben zu minimieren hängt von sich ständig wechselnden Parametern ab wie Energiekosten, geplante und ungeplante Neuinvestitionen und vielen Weiteren. Selbst bei dem zitierten Brettspielabend hängt der eigene nächste Zug von schon getätigten als auch von den folgenden ab, welches bei den meisten Spielen in Gänze kaum überblickbar oder berechenbar ist.
Ein Unternehmen unterscheidet sich nicht stark vom privaten Leben. Man ist ständig konfrontiert mit der Optimierung von Ressourcen, Energie, Gewinn, Aufwand, Investitionsentscheidungen unter sich ständig ändernden äußeren Einflüssen oder den Entscheidungen seiner Marktbegleiter. Als wenn das nicht genug wäre, widersprechen sich manche äußeren Bedingungen wie die Produktion optimal auszulasten, aber am liebsten ohne Energieverbrauch oder das hergestellte Produkt günstig auf den Markt zu platzieren, aber den Gewinn zu maximieren.
Hier stellt sich die Frage, wie solche Probleme mathematisch überhaupt formuliert werden können. Falls ein oder sogar mehrere optimale Zustände unter den vielen Bedingungen und Voraussetzungen gefunden wird, kann das Ergebnis überhaupt interpretiert, umgesetzt und genutzt werden? Wie rechenintensiv und komplex ist das alles und lohnt sich das?
Auf alle Fragen können wir mit Sicherheit sagen: Ja. Neugierig geworden? Na, dann haben wir ja unser Optimum erreicht.
ROUTENPLANUNG

- Gesucht: Minimiere Transportkosten.
- Challenges: Ein Problem voller Widersprüche: Distanzärmste im Widerspruch zur zeitärmsten Strecke, ökonomisch günstigste im Widerspruch zur treibstoffärmsten Route. Dazu die Einhaltung der Lieferungen in Zeitfenstern, Berücksichtigung von Kapazitäten.
- Lösung: Schnelle und optimale Lösungsfindung mit Hilfe der richtigen Methodik der Mathematik.
AUTONOMES FAHREN

- Gesucht: Finde Fahrsituationen, welche am risikoreichsten sind.
- Challenges: Was bedeutet Risiko und wie wird es berechnet? In welchem Bereich wird es gesucht? Wie findet man alle risikoreichen Stellen?
- Lösung: Strategische, zufallsbestimmte Stichprobenentnahme zur Auffindung risikoreicher Fahrsituationen.
ZEITPLAN ERSTELLUNG
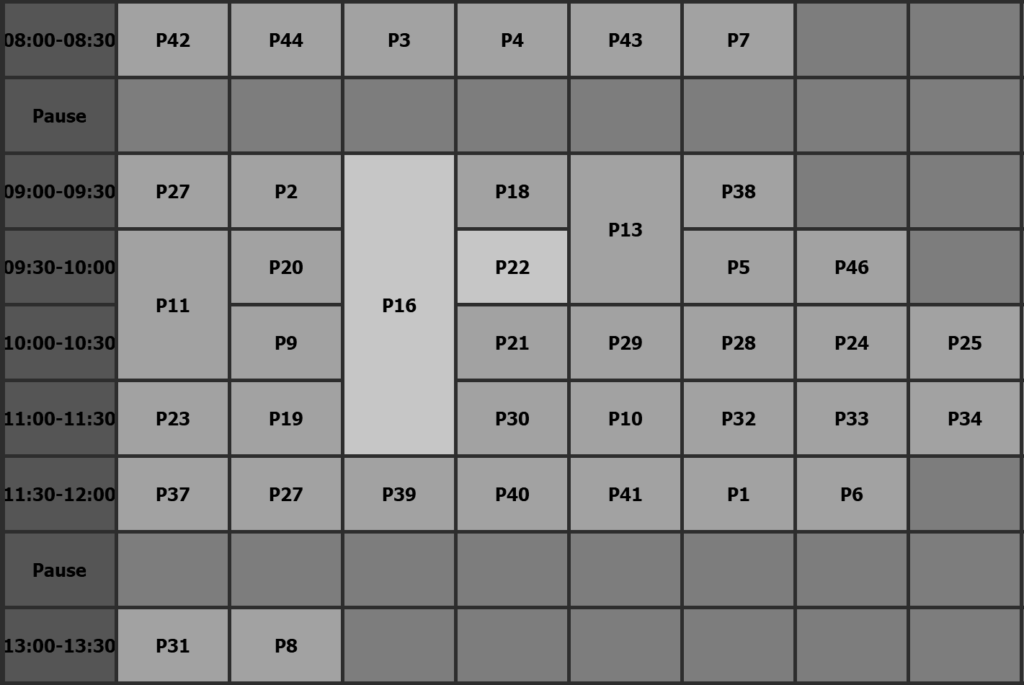
- Gesucht: Optimale Ressourcen- und Materialallokation in vorgegebenen Zeitfenstern.
- Challenges: Material und Ressourcen stehen begrenzt zur Verfügung. Komplexität an möglichen Kombinationen sind extrem hoch.
- Lösung: Schnelle Optimierung mit visuellem, anwendbarem Resultat.
QUANTEN COMPUTER

Kurz: ein neuartiges Forschungsgebiet mit hohem Zukunftspotential.
Lässt sich damit jedes Problem schneller lösen? Leider nein, nicht einmal jedes Problem ist für einen Quantencomputer geeignet, geschweige denn schneller lösbar. Wie könnte das Potential eines Quantencomputers jetzt schon genutzt werden? Lassen Sie uns das gemeinsam herausfinden und mögliche Einsatzfelder definieren, sowie mögliche vorhandene Probleme in die Welt der Quantencomputer überführen. Lassen Sie uns die Vorteile, sowie prognostizierbare Effizienzsteigerungen erforschen.